[Hegelians] observe, correctly, that contradictions are of the greatest importance in the history of thought--precisely as important as criticism. For criticism invariably consists in pointing out some contradiction; either a contradiction between the theory and another theory which we have some reason to accept, or a contradiction between the theory and certain facts--or more precisely, between the theory and certain statements of fact. Criticism can never do anything except either point out some such contradiction, or, perhaps, simply contradict the theory (i.e. the criticism may be simply the statement of the antithesis). But criticism is, in a very important sense, the main motive force of any intellectual development. Without contradictions, without criticism, there would be no rational motive for changing our theories: there would be no intellectual progress.
Karl Popper, Conjectures and Refutations, chapter 15
I
I propose that there are two major forces that guide a mind's evolution over time: the drive for explanatory power, and the drive for consistency. A mind wants to be able to explain reality, but also wants to ensure that it's explanations don’t entail any contradictions. There exists a tension between these two drives, and the goal of creative thought is to search for a way to overcome this tension.
It's trivial to find ideas with high explanatory power if we don't care about those ideas being inconsistent: we can just blindly invent a wide variety of explanations, accept all of them, and in short time we find some explanation for anything we care about. It's only when we require ourselves to be consistent - to not accept sets of ideas that entail contradictions - that it becomes non-trivial to find a set of ideas with explanatory power. Similarly, it's trivial to find a consistent set of ideas if we don't care about the set having any explanatory power: simply adopt the empty set, i.e. don't accept any ideas. Only in the context of a desire for explanatory power does criterion of consistency become non-trivial.
The drives for explanatory power and consistency allow us to define a partial ordering over all possible sets of ideas. An intelligent mind can be thought of as an algorithmic system that attempts to climb this partial ordering through a process of conjecture and criticism.
II
Let a worldview be a set of ideas that represents a complete, independent attempt to explain reality. The explanatory power of a worldview can be identified with the set of questions that it can answer for us, or, more specifically, the set of questions it can answer that we actually care about answering. Having multiple answers to a question doesn't add anything to a worldview's explanatory power compared to just having one answer. Explanatory power is just a measure of the questions that the worldview gives us some answer too.
Let E(W) denote the explanatory power of a worldview W. E(W) is the set of questions that W answers. There are three different relationships that two worldviews A and B might have, in terms of explanatory power:
A and B might be equivalently powerful, meaning they answer exactly the same set of questions: E(A)=E(B)
A might be more powerful than B (or vice versa), meaning the set of questions that A answers is a strict superset of the questions that B answers: E(A)⊃E(B)
A and B might be incomparably powerful, meaning they are neither equivalently powerful nor is either more powerful than the other: E(A)⊅E(B) and E(A)⊄E(B)
Let I(W) denote the set of inconsistencies - pairs of directly contradictory statements - that a worldview W entails. As with explanatory power, there are three relationships that two worldviews A and B might have with respect to their inconsistencies: they might be equivalently inconsistent (I(A)=I(B)), one might be more inconsistent than the other (I(A)⊃I(B)), or they might be incomparably inconsistent (I(A)⊅I(B) and I(A)⊄I(B)).
A worldview A is strictly superior to another worldview B when one or both of the following conditions hold:
A is either equivalently powerful to B or more powerful than B, and B is more inconsistent than A.
A is more powerful than B, and B is either equivalently inconsistent to A or more inconsistent than A.
In other words, a worldview A is strictly superior to another B if either: 1) A can answer every question that B can answer but A doesn’t entail some of the contradictions that B entails (or any other contradictions), or 2) A can answer every question that B answers in addition to some other questions while not entailing any contradictions that B does not entail. More succinctly, a worldview A is strictly superior to a worldview B, denoted A > B, if and only if the following three conditions hold:
E(A) ⊇ E(B)
I(A) ⊆ I(B)
E(A) ⊃ E(B) or I(A) ⊂ I(B)
III
The strict superiority relation forms a strict partial order over the set of all worldviews. An intelligent mind is an evolutionary system that attempts to climb this partial ordering. A mind consists mainly of a set of worldviews. The mind evolves over time by blindly generating a wide variety of novel worldviews, and rejecting worldviews that prove to be strictly inferior to others. By iterating this process of generating new worldviews and rejecting inferior ones, the mind effectively searches for worldviews that maximize explanatory power while minimizing inconsistency.
Karl Popper argued that intellectual progress happens through an iterative process of conjecture and criticism. The two steps of the iterative process described in the previous paragraph can be identified with the Popperian notions of conjecture and criticism, respectively. Conjecture is a process of blindly generating a novel worldview, and criticism is a process of narrowing down a population of worldviews by rejecting those that are strictly inferior to others.
I have said several times that conjecture works by blindly generating new worldviews. More specifically, I suggest that conjecture can be understood as a process by which the mind randomly varies its existing worldviews to produce new ones. This process is closely analogous to the biological process of genetic mutation. Because the conjectured worldviews are created by random variation, the vast majority of them will inevitably turn out to be useless, just as the vast majority of mutant genes are useless. But just as natural selection removes detrimental genes from the gene pool, leaving behind only those genes which are relatively well-adapted to their environment, criticism will remove inferior conjectures from the mind, leaving only those worldviews which maximize explanatory power while minimizing inconsistency.
Computationally speaking, genes are essentially strings, and genetic mutation can be understood as an algorithm that modifies these strings to produce new ones. Worldviews, however, have a different structure: they are not strings, but sets of ideas. The details of the process by which new worldviews are generated must, therefore, be somewhat different than the details of the process of biological mutation, and of traditional genetic algorithms. A newly conjectured worldview created by varying an existing one should presumably contain most of the same ideas as the old worldview, but perhaps with a few ideas removed, and/or a few new ones included. Clearly there are many other details of the process of variation that are left to be filled in, but for brevity I will reserve the discussion of these details for a future post.
Criticism, in contrast to conjecture, can be fully described in a relatively simple way. Given a set of worldviews M within a mind, criticism is a process of removing worldviews from M that are strictly inferior to other worldviews in M. In other words, criticism involves replacing the mind’s set of ideas M with a set M’⊂M such that:
A mind evolves by continuously cycling between the processes of conjecture and criticism. First the mind expands it’s set of worldviews via conjecture, and then it narrows down it’s set of worldviews via criticism. To understand how this process helps a mind discover better worldviews, let’s consider a single cycle of conjecture and criticism and explore the various ways that it may play out.
Suppose that before some particular cycle of conjecture and criticism, the mind has a set of worldviews M. Then, the mind conjectures some new worldview W’ by blindly varying one or more of the worldviews in M, and thus it expands it’s set of worldviews to be M ∪ {W’}, which I will denote M⁺. Then, the mind removes any worldviews from M⁺ that are strictly inferior to others (using the above formula, but with M⁺ in place of M) to produce a final set M’. At this point, the cycle of conjecture and criticism is over, and the mind begins again by conjecturing a new worldview.
There are three distinct scenarios that may happen when narrowing down M’ to produce M⁺. First, W’ could be strictly inferior to one or more worldviews in M. In this case, the mind will immediately reject the newly conjectured worldview, in the sense that the mind will remove W’ from M⁺ during criticism, so M’ = M. Second, W’ could be neither strictly inferior or strictly superior to each other worldview in W. In this case, the mind will tentatively accept W’ as a worldview worth keeping around, and thus M’ = M⁺. Finally, W’ could be strictly superior to some of the existing worldviews in M. In this case, the mind will not only tentatively accept W’, but also reject the old worldviews that are inferior to W’, and so M’ will be a subset of M⁺ containing W’ and whichever worldviews from M that are not inferior to W’.
IV
In defining the strict superiority relation, I relied on the constructs E(W) and I(W) to represent the explanatory power of a worldview and inconsistencies within a worldview, respectively, but I have not yet formally defined them. In a previous post I introduced a formalism for inferential reasoning which I will now use to define E(W) and I(W) more explicitly.
I have said that a worldview is a set of “ideas”, but more precisely, I will treat a worldview as a set of statements. A mind is equipped with an inference rule which it uses to work out the consequences of the statements within it’s worldviews. Given an inference rule r, the set of consequences of a worldview W is given by Fᵣ ᪲(W), and for short I will denote this C(W). The explanatory power and inconsistency of a worldview W can each be defined in terms of C(W).
To define the inconsistency of a worldview I(W), we will have to introduce some additional structure to the statement universe, which I will call U. “Inconsistency” or “Contradiction” is a well-defined concept in the context of classical logic, but the formalism I’m describing does not make use classical logic, but rather a much broader framework of inferential reasoning. To define the notion of a “contradiction” in our context, I will assume that each statement in the statement universe U has a “negation” - some other statement in the universe that has exactly the opposite semantic meaning. In other words, for every statement “p”, there will be some statement “not p”. A worldview is inconsistent when it’s consequences contain two statements that are negations of one another. If we denote the negation of some statement s as ¬s, we can define the set of inconsistencies within a worldview I(W) as:
The explanatory power of a worldview E(W) is equivalent to the set of questions that W allows the mind to derive an answer to (that it actually cares to answer). For the purpose of defining explanatory power, I will treat a “question” as a predicate over the statement universe U, or in other words, a function that returns a True of False value for each possible statement. A worldview W answers a question q when q returns True for at least one of the consequences of W. Therefore, if the mind has a set of questions Q that it wants to answer, the explanatory power of a worldview W is:
V
As I said in the previous section, each mind is equipped with some kind of inference rule. For a mind to be generally intelligent, it must, I propose, use a computationally universal inference rule - a rule capable of simulating all other computable inference rules. A mind with such an inference rule will be capable, if it conjectures the right set of statements, of acting as though it had any other computable inference rule. A mind with a universal inference rule will, therefore, effectively be able to conceive of any worldview (in the sense of being able to work out the consequences of the worldview) that any other mind could possibly conceive of. Thus, when a mind with a universal inference rule searches for new worldviews through the process of conjecture and criticism, we can formally guarantee that the space through which it searches is as large as and inclusive as it could possibly be; it is effectively the space of all worldviews conceivable by any possible mind. In this sense, a mind equipped with a universal inference rule would be, to use David Deutsch’s terminology, a universal explainer.

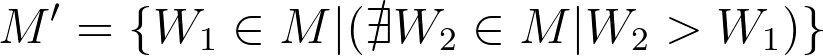
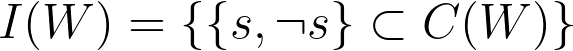
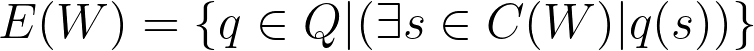
> A mind wants [...] to ensure that it's explanations don’t entail any contradictions.
its
> First the mind expands it’s set of worldviews via conjecture, and then it narrows down it’s set of worldviews via criticism.
Same, twice. Also in:
> thus it expands it’s set
> within it’s worldviews
Then:
> does not make use classical logic
of
Overall, I cannot tell if you describe an intelligent mind or any mind. If I just focus on the words you use, you seem to switch between the two. On the one hand, you write:
> I propose that there are two major forces that guide a mind's evolution over time: the drive for explanatory power, and the drive for consistency. A mind wants to be able to explain reality, but also wants to ensure that it's explanations don’t entail any contradictions.
But you also write:
> An intelligent mind can be thought of as an algorithmic system that attempts to climb this partial ordering through a process of conjecture and criticism.
And here's an example of a switch between two consecutive sentences:
> An intelligent mind is an evolutionary system that attempts to climb this partial ordering. A mind consists mainly of a set of worldviews.
So which are you interested in explaining: intelligent minds or minds in general?
The Popper quote at the beginning, what edition is that from? Looks like it may be a misquote. See this diff https://jsbin.com/vubecuxapu/edit?output based on https://www.google.com/books/edition/Conjectures_and_Refutations/fZnrUfJWQ-YC?hl=en&gbpv=1&bsq=%22observe,%20correctly%22